哈勃–勒梅特定律

在物理宇宙学里，哈勃–勒梅特定律（英语：Hubble-Lemaître law）指遥远星系的退行速度与它们和地球的距离成正比，换句话说，离我们越遥远的星系，远离我们的速度越快。通常天文学家通过测量红移，也就是星系发出的光的波长的变化，来测定星系的退行速度。

这条定律原先称为哈勃定律（英语：Hubble's law），以证实者埃德温·哈勃的名字命名；2018年10月经国际天文联合会表决通过更改为现名，以纪念更早发现宇宙膨胀的比利时天文学家乔治·勒梅特。它被认为是空间尺度扩展的第一个观察依据，今天经常被援引作为支持大爆炸的一个重要证据。

埃德温·哈勃最早于1929年发表了哈勃定律，但是用来描述宇宙以一定速度膨胀的数学公式，即弗里德曼方程，则是由亚历山大·弗里德曼于1922年从广义相对论中推导得到的。在哈勃之前，天文学家卡尔·维尔兹在1922及1924年在自己获得的观测数据中发现表面上更小更暗的星系的红移更高，这可能暗示离我们更远的星系以更快的速度远离我们。1927年，乔治·勒梅特注意到遥远星体的退行速度和它们与地球间的距离呈正比关系，并据此指出宇宙可能在膨胀。勒梅特当时估算了这个正比系数，而哈勃两年后确认了宇宙膨胀这一事实并测量计算得到更精确的值，因而这个系数后来被称为哈勃常数。1912年，亨丽爱塔·斯万·勒维特发现了造父变星的周光关系，之后这一关系被天文学家用于测量星系的距离。而在1917年，维斯托·斯莱弗就测量了许多天体的红移并将其与它们的速度联系在一起。哈勃沿用了这些方法并获得了更多观测数据，在此基础上测得了当时最精确的宇宙膨胀率。

在宇宙学研究中，哈勃-勒梅特定律成为宇宙膨胀理论的基础，以方程表示

$v=H_{0}D$ ；

其中，$v$ 是由红移现象测得的星系远离速率，$H_{0}$是哈勃常数，$D$是星系与观察者之间的距离。

哈勃常数常以千米/秒/百万秒差距（km/s/Mpc）为单位表述，其值70对应着距离一百万秒差距（3.09×10¹⁹千米）的星系以每秒70千米的速度退行。简化量纲后，$H_{0}$的单位实为赫兹（Hz），即表征时空膨胀速率的频率，因此其倒数被称作哈勃时间（144亿年）。该常数亦可解读为相对膨胀率——以7%/十年为单位，意味着在现行膨胀速率下，任一无约束宇宙结构需历经十亿年方能增长7%。

发现

哈勃常数的函数图像

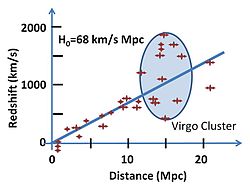
1912年到1922年间，美国天文学家维斯托·斯里弗观测了41个星系的光谱，发现其中的36个星系的光谱发生红移，他认为这种现象意味着这些星系正在远离地球。

1916年，爱因斯坦提出了广义相对论。许多物理学家和数学家利用爱因斯坦场方程建立了时间和空间协调一致的理论。将最一般的原则应用到自然的宇宙，产生了一个动态的解决方案，与当时的静态宇宙的概念产生了冲突。

1922年，亚历山大·弗里德曼基于爱因斯坦场方程，推导出描述宇宙演化的弗里德曼方程，这项工作揭示出宇宙可能正处于膨胀状态，且其膨胀速率可以通过该精确计算。弗里德曼引入了如今被称为尺度因子的核心概念，可视为哈勃定律比例常数的标度不变形式。该方程体系的建立，本质上是通过将均匀且具有各向同性的宇宙模型代入爱因斯坦场方程，并引入特定密度和压力的流体假设而实现的。这种时空膨胀的概念最终催生了宇宙学的大爆炸理论和稳恒态理论。

1927年，即哈勃发表其研究成果的两年前，比利时神父兼天文学家乔治·勒梅特已率先发表论文，首次推导出哈勃–勒梅特定律。加拿大天文学家西德尼·范登贝格指出："勒梅特关于宇宙膨胀的发现最早于1927年以法文发表于某低影响力期刊，但在1931年影响力更大的英译版本中，涉及现今所称哈勃常数的关键方程相比原版有所修改"。现有证据表明，这些译文修改行为系勒梅特本人所为。

哈勃的工作

埃德温·哈勃的主要天文观测工作均在威尔逊山天文台完成，该台当时拥有全球最先进的天文望远镜。1924年，他通过观测"旋涡星云"中的造父变星，成功计算出这些天体的距离。令人惊讶的是，这些天体的与我们的距离远超银河系范围， 是银河系外的独立天体。尽管当时学界仍沿用"星云"这一旧称，但后来该术语逐渐被"星系"取代。这标志着人类对宇宙结构认知的根本性转变。

哈勃定律中涉及的星系退行速度和距离并非直接测量得出。退行速度通过辐射红移值z = ∆λ/λ 推算，距离则通过天体亮度估算。哈勃致力于建立天体亮度与红移参数z之间的定量关系。1929年，通过整合自己的星系距离测量数据，以及维斯托·斯里弗和米尔顿·赫马森获得的对应星系红移值，哈勃发现天体红移与其距离之间存在粗略的正比关系。尽管数据中存在显著的方差（现已知由本动速度导致——"哈勃流"特指远离本动速度影响、以宇宙膨胀为主导的遥远空间区域），哈勃仍基于46个星系样本绘制出趋势线，得出哈勃常数值为500 (km/s)/Mpc。由于距离标定中的误差，该数值明显高于当前公认的约70 (km/s)/Mpc（详见宇宙距离尺度）。

说明

因发现远离速度与距离呈线性关系，而产生哈勃定律，其线性数学式如后：

$v=H_{0}D$

其中$v$是由红移现象测得的远离速率，一般表示为km/s。H₀是哈勃常数，在弗里德曼方程中对应着数值$H$（通常称为哈勃参数，是一个取决于时间的值，由时间的观测得来，以下标0来区别。）此常数在宇宙中对任意保角时间（conformal time）而言皆是相同的。$D$是光相对于观测者的惯性坐标系穿越星系的适当距离，以百万秒差距（Mpc）作为测量单位。

对于相对邻近的星系，速度v可从星系的红移z利用红移公式$v=zc$估计，其中c是光速。对遥远的星系，速度v可以从红移z利用相对移动的多普勒效应决定。然而，最好的方法来计算远离速度及其相关时空膨胀率是考虑来自远星系光子的相关保角时间。对于非常遥远的星体，退离速度可能大于光速。但是这并不违反狭义相对论，因为度量空间的扩张并不与任何有形物体的速度相关。

当使用哈勃定律来决定距离时，只能用因宇宙膨胀而造成的速度。引力相互作用星系的运行与彼此相关，而独立于宇宙膨胀之外。因其相对运行所造成的这类相对速度，被称作本动速度（peculiar velocities）。当使用哈勃定律时，本动速度需要加入考虑。1938年，Benjamin Kenneally所发现的“上帝的手指”效应（Fingers of God）是本动速度所造成的现象之一。受引力约束的系统，例如星系或我们的行星系统，都不会受到哈勃定律的影响，也不会膨胀。

针对均匀膨胀的宇宙的理想哈勃定律，其数学推导是一个在三维笛卡尔/牛顿协调空间相当初等的几何定理。此协调空间被视为一种度量空间，具有完全均匀和各向同性（性质不随地点或方向改变）。简单说明该定理如下：

对于任何正沿直线远离原地，速度与离开距离成正比的两点，将以正比于两者距离的速度远离对方。

宇宙的最终命运和宇宙的年龄，可以取决于测量现今的哈勃常数和推断减速参数的观测值，此参数特具密度参数值（Ω）的特征。所谓的“封闭宇宙”（Ω＞1）即将在一次“大紧缩”（Big Crunch）后结束，比哈勃年龄年轻。“开放宇宙”（Ω≦1）永远都在扩张且具有较接近哈勃年龄的年龄。我们所居住的宇宙为“加速宇宙”（accelerating universe），其年龄正巧非常接近哈勃年龄。

哈勃常数的值随着时间变化，其增加或减少取决于减速参数$q$的正负，$q$定义为：

$q=-H^{-2}\left({{\;dH} \over {\;dt}}+H^{2}\right)$

在减速参数为零的宇宙，有H = 1/t，其中t是自大爆炸以来的时间。然而，非零且与时间相关的$q$值，则需要积分弗里德曼方程，将时间倒退到粒子视野（particle horizon）为0时（即大爆炸之初）。

我们可以定义宇宙的“哈勃年龄”（又称为“哈勃时间”或“哈勃期”）为1/H，或9777.93（亿年/[H/(km/s/Mpc)]）。哈勃年龄以H=70 km s⁻¹ Mpc⁻¹来计算为139.68亿年，或以H=71 km s⁻¹ Mpc⁻¹计算得137.72亿年。当星系的红移z很小时，与我们的距离大约是zc/H，其中c是1（光年／年），又此距离可以被简单地以z（红移）时间表示为137.72亿光年。

长久以来q被认为是正值，这表示由于引力的作用，宇宙膨胀正在减慢。这意味着宇宙的年龄小于1/H（约140亿年）。例如，若q为1/2时（其中一个理论上的可能值），宇宙的年龄为2/(3H) 。在1998年，一项发现指出q显然是负值，代表着宇宙其实比1/H还要老。事实上，估计的宇宙年龄相当接近1/H。

奥伯斯佯谬

主条目：奥伯斯佯谬

哈勃定律对大爆炸的解释总结了空间的扩展与著名的古老难题奥伯斯佯谬之间的矛盾：如果宇宙是无限的、稳定的，充满了均匀分布的恒星，那么在天空中视线所及之处都将存在着恒星，而天空也将会像恒星的表面一样明亮。从1600年代开始，天文学家和其他的思想家提出了许多可能解决这个佯缪的想法，但当前能被接受的这一部分是来自大爆炸的理论。宇宙只存在了有限的时间，只有有限多的星光有机会到达我们这儿，所以矛盾就解决了。换言之，在膨胀的宇宙中，远方天体的远离速度使来自她们的星光产生红移并且降低了亮度，但这样也只是解决了部分的矛盾。依照大爆炸的理论，两者都有贡献（宇宙的历史是有限的在两者中较为重要）。 天空之所以黑暗，也为大爆炸提供了一种证据。

哈勃常数的测量

哈勃常数的值通常经由遥远星系的红移来测量，这就是用与哈勃定律不同的方法测量同一星系的距离。但是在用来测量这些距离的物理假设上的不确定，造成哈勃常数的值有不同结果的。在20世纪的后半期，多数的哈勃常数值$H_{0}$都被估计在50和90 km s⁻¹ Mpc⁻¹之间。

哈勃常数的数值无法直接测量，而是通过结合天文观测数据和模型间接推导得出。过去几十年来，日益精确的观测与新模型的提出使得科学家获得了两组高度精确的数值，但这两组结果并不一致。这种测量差异现在被称为“哈勃常数危机”。

对哈勃常数的争论

“ 天文物理经常都是错的，但从未被怀疑过。 ... 罗伯特·科什纳 ”

哈勃常数的值曾是个长久而激烈的争议主题，热拉尔·佛科留斯主张其值应为100而艾伦·桑德奇则认为其应为50附近。

1996年，由约翰·诺利斯·巴寇主持，包含古斯塔夫·安德列斯·塔曼及薛尼·范德胡斯特以类似早期沙普利-柯蒂斯之争的模式举行，针对上述两个竞争数值进行辩论。

1990年代晚期，引进宇宙的λ-CDM模型，数值差异的问题获得部分的解决。

精确宇宙学和哈勃常数危机

自20世纪90年代末以来，理论和技术的进步使得更高精度的测量成为可能。然而，两大类别的高精度测量方法却在哈勃常数具体数值上存在统计显著的差异。使用校准宇宙距离阶梯技术进行的"晚期宇宙"测量获得的$H_{0}$逐渐趋近于约73 km s⁻¹ Mpc⁻¹的数值。自2000年以来，宇宙微波背景等手段测量的“早期宇宙”技术逐渐得到应用，这些方法给出的$H_{0}$数值接近67.7 km s⁻¹ Mpc⁻¹。最初，这种差异在估计的测量误差范围内，因此在当时并未引起很大关注。但随着技术的改进，估计的测量误差范围已逐渐缩小，但两种方法测得的$H_{0}$差异却未减少，导致目前这种差异在统计意义上已具有高度显著性。因此这一差异被称为“哈勃常数危机”。

作为"“早期测量”的一个示例，普朗克卫星2018年公布的测量$H_{0}$值为67.4±0.5 km s⁻¹ Mpc⁻¹。在“晚期测量”中，科学家通过哈勃空间望远镜测得了更高值74.03±1.42 km s⁻¹ Mpc⁻¹，并且这一结果于2023年由通过詹姆斯·韦伯空间望远镜获得的数据得到进一步确认。这些"早期"和"晚期"测量结果的差异达到大于5 σ的水平，远超出合理的偶然误差范围。如何解决这一分歧仍是当前活跃的研究领域。

截至2021年的哈勃常数测量概况，其中2018年宇宙微波背景（“早期测量”）测量结果及误差范围以粉红色涂色区域显示，2020年造父变星-Ia超新星距离阶梯（“晚期测量”）测量数值及误差范围以青色涂色区域显示。  

使用哈勃太空望远镜的值

哈勃关键计划（由在卡内基天文台的Wendy L. Freedman博士主导）使用哈勃太空望远镜进行最精确的光学测量，在2001年五月，发表其最终估计值为72±8 km s⁻¹ Mpc⁻¹，此结果与基于苏尼亚耶夫-泽尔多维奇效应进行的银河系星群观测所测出的$H_{0}$相当一致，具有相似的精确值。

使用WMAP的资料

在2003年，利用WMAP所得出最高精度的宇宙微波背景辐射测定值为71±4 km s⁻¹ Mpc⁻¹，而在2006年，精确度提升至70.4 +1.5
−1.6 km s⁻¹ Mpc⁻¹，2008年T，WMAP在线上提供的数值是71.9 +2.6
−2.7 km s⁻¹ Mpc⁻¹.[1]。 这些来自WMAP和其他宇宙论的数值都与简单版本的λ-CDM模型日趋接近。如果这些数值能与更普遍的版本吻合，$H_{0}$倾向于更小和更不确定：通常数值在67 ± 4 km s⁻¹ Mpc⁻¹的附近，但有些模型的数值接近63 km s⁻¹ Mpc⁻¹。

使用钱卓X射线天文台的资料

在2006年8月，来自马歇尔太空飞行中心（MSFC）的研究小组使用美国国家航空航天局的钱卓X射线天文台利用苏尼亚耶夫-泽尔多维奇效应测量的的$H_{0}$值是 76.9 +10.7
−8.7 km s⁻¹ Mpc⁻¹。

加速膨胀

在1998年，来自Ia超新星标准烛光测量的$q$值却是负数，令许多天文学惊讶的是宇宙加速膨胀，虽然哈勃因子会随着时间而衰减。请参见暗物质和ΛCDM模型。

2009年5月7日，美国宇航局发布最新的哈勃常数测定值，根据对遥远星系Ia超新星的最新测量结果，常数被确定为74.2± 3.6 km s⁻¹ Mpc⁻¹，不确定度进一步缩小到5%以内。

2012年10月3日，天文学家使用美国宇航局的斯皮策红外空间望远镜精确计算了哈勃常数，数值结果为74.3±2.1 km s⁻¹ Mpc⁻¹。

2012年12月20日，美国国家航空航天局的威尔金森微波各向异性探测器实验团队宣布，哈勃常数为69.32 ± 0.80 km s⁻¹ Mpc⁻¹。

2013年3月21日，从普朗克卫星观测获得的数据，哈勃常数为 67.80 ± 0.77 km s⁻¹ Mpc⁻¹。

2018年7月，利用哈勃望远镜和盖亚任务，测得哈勃常数值为 73.52 ± 1.62 km s⁻¹ Mpc⁻¹。

2018年，普朗克卫星最终测得哈勃常数值为 67.66±0.42 km s⁻¹ Mpc⁻¹。

2021年，SH0ES合作组利用造父变星-Ia型超新星宇宙距离阶梯方法测得的哈勃常数值为 73.04±1.04 km s⁻¹ Mpc⁻¹。2022年， Pantheon+合作组在此基础上使用另一个Ia型超新星样本测得的哈勃常数值为 73.4 +0.99
−1.22 km s⁻¹ Mpc⁻¹。

2023年7月13日，南极望远镜（SPT-3G）通过对微波背景辐射的温度和偏振（TT/TE/EE）能谱的观测测得的哈勃常数值为 68.3±1.5 km s⁻¹ Mpc⁻¹。

哈勃危机的潜在解决方案

哈勃危机的成因尚不明确，学界提出了许多可能的解决方案。最保守的解释是，早期宇宙或晚期宇宙的观测中可能存在某种未知的系统误差。尽管这一解释在直觉上颇具吸引力，但无论问题出在早期还是晚期宇宙观测，它都需要假设多个互不关联的误差源同时存在，而目前尚未发现符合条件的明确候选因素。此外，由于早期和晚期宇宙观测数据均来自多台不同的望远镜，任何此类系统误差都需能影响多种独立仪器。

另一种可能是观测本身准确无误，但存在未被考虑的因素导致了这种差异。如果宇宙学原理（即宇宙是均匀且具有各向同性的）失效，那么目前对哈勃常数及哈勃张力的解释将需要修正，这可能化解哈勃张力。特别需要指出的是，若要此类解释与超新星及重子声学振荡观测相吻合，我们所在的位置需要处于一个延伸至红移约0.5的巨大宇宙空洞之中。另一种潜在解释是测量中的不确定性可能被低估，但考虑到各测量结果之间的内部一致性，这种可能性既不高，也无法完全解释整体的张力现象。

最后一种可能性涉及超越当前公认宇宙学模型（ΛCDM模型）的新物理学理论。这类理论非常丰富，例如用修正引力理论取代广义相对论可能解决该张力；此外，在早期宇宙中更强暗能量成分，具有时变状态方程的暗能量，或是衰变为暗辐射的暗物质等设想也具可行性。 所有这类理论面临的共同挑战在于，早期和晚期宇宙测量均依赖多个独立物理理论体系，在保持现有理论其他领域成功解释力的同时，要修改其中任一体系都极为困难。某些学者指出单凭早期宇宙新物理并不足够，而另一些研究则表明仅靠晚期宇宙新物理也难以奏效，这种争议恰好体现了该问题的复杂程度。尽管如此，自2010年代中期以来，随着学界对哈勃张力的关注度持续升温，天文学家们仍在不断探索新的解决路径。

哈勃常数的推导

从弗里德曼方程开始：

$H^{2}\equiv \left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G}{3}}\rho -{\frac {kc^{2}}{a^{2}}}+{\frac {\Lambda }{3}},$

此处$H$是哈勃参数，$a$是宇宙标度因子，$G$是万有引力常数，$k$是标准化的宇宙空间曲率，其值为 −1、0、或 +1，和$\Lambda$是宇宙常数。

物质主导的宇宙(和宇宙常数)

如果宇宙是物质主导，则宇宙的质量密度$\rho$ 刚好可以包括的物质是

$\rho =\rho _{m}(a)={\frac {\rho _{m_{0}}}{a^{3}}},$

此处$\rho _{m_{0}}$是现在的物质密度，我们知道的非相对论粒子质量密度会随着宇宙的体积增加而成比例的降低，所以上述方程必须为真。我们也可以定义(参见$\Omega _{m}$的密度参数)：

$\rho _{c}={\frac {3H^{2}}{8\pi G}};$

$\Omega _{m}\equiv {\frac {\rho _{m_{0}}}{\rho _{c}}}={\frac {8\pi G}{3H_{0}^{2}}}\rho _{m_{0}};$

所以$\rho =\rho _{c}\Omega _{m}/a^{3}.$也可以，依据定义：

$\Omega _{k}\equiv {\frac {-kc^{2}}{(a_{0}H_{0})^{2}}}$

和

$\Omega _{\Lambda }\equiv {\frac {\Lambda c^{2}}{3H_{0}^{2}}},$

此处的下标0代表现在的数值，并且$a_{0}=1$。到此为止的所有一切都是章节刚开始的弗里德曼方程和转换$a$ 成为 $a=1/(1+z)$ 得到

$H^{2}(z)=H_{0}^{2}\left(\Omega _{M}(1+z)^{3}+\Omega _{k}(1+z)^{2}+\Omega _{\Lambda }\right).$

物质和暗能量主导的宇宙

如果宇宙是物质主导和暗能量主导，然后前述方程中的哈勃参数也将是暗能量的状态方程。所以现在：

$\rho =\rho _{m}(a)+\rho _{de}(a),$

此处$\rho _{de}$是暗能量的质量密度。依据定义，在宇宙论的状态方程是$P=w\rho c^{2}$，并且我们将这带入流体的方程，它描述了宇宙的质量密度随着时间的变化，

${\dot {\rho }}+3{\frac {\dot {a}}{a}}\left(\rho +{\frac {P}{c^{2}}}\right)=0;$

${\frac {d\rho }{\rho }}=-3{\frac {da}{a}}\left(1+w\right).$

如果w 是常数，

$\ln {\rho }=-3\left(1+w\right)\ln {a};$

$\rho =a^{-3\left(1+w\right)}.$

那么暗能量就是w状态的恒等式，$\rho _{de}(a)=\rho _{de0}a^{-3\left(1+w\right)}$。如果我们以与之前相似的方式转换弗里德曼方程，但是这次设定$k=0$，这是假设我们生活在一个平坦空间的宇宙 (参见宇宙的形状)，

$H^{2}(z)=H_{0}^{2}\left(\Omega _{M}(1+z)^{3}+\Omega _{de}(1+z)^{3\left(1+w\right)}\right).$

如果暗能量不是w状态的恒等式，则

$\rho _{de}(a)=\rho _{de0}e^{-3\int {\frac {da}{a}}\left(1+w(a)\right)},$

要解此方程，我们需要参数化$w(a)$，例如如果 $w(a)=w_{0}+w_{a}(1-a)$，得到

$H^{2}(z)=H_{0}^{2}\left(\Omega _{M}a^{-3}+\Omega _{de}a^{-3\left(1+w_{0}+w_{a}\right)}e^{-3w_{a}(1-a)}\right).$

由哈勃常数导出的单位

哈勃时间

哈勃常数$H_{0}$的单位是时间的倒数，也就是说$H_{0}$ ~ 2.27×10⁻¹⁸ s⁻¹。“哈勃时间”定义为$1/H_{0}$。在标准宇宙论模型的哈勃时间是4.55×10¹⁷ s 或144亿年，"扩张时间尺度"一词的意思是"哈勃时间"[2]（页面存档备份，存于互联网档案馆）。如果$H_{0}$的值保持恒定，哈勃时间自然的解释是电子大小的宇宙增加一个数量级所需要的时间 (因为解dx/dt = x$H_{0}$ is x = $s_{0}$exp($H_{0}$t)，此处$s_{0}$是在t = 0的任意初始条件下的形状)。但是，在如上文所述的广义相对论、暗能量、暴胀等，长时间下的动力学是复杂的。

哈勃长度

哈勃长度是宇宙论的距离单位，定义为$c/H_{0}$—光速与哈勃时间的乘积。它相当于42亿2800万秒差距或138亿光年(哈勃长度以光年表示的数值，依据定义，等同于哈勃时间以年表示的值)。

哈勃体积

哈勃体积有时被定义为共动大小$c/H_{0}$的体积。精确的定义是：有时将其定义为球体半径为$c/H_{0}$时的体积。有些宇宙论甚至使用哈勃体积一词引用为可观测宇宙的体积，然而这个半径可能还要大3倍。

参见

• 宇宙的年龄
• 宇宙形状
  • 双曲线几何 (空间因膨胀而弯曲)
  • 欧几里得几何 (空间因平衡而平坦)
  • 椭球几何 (空间因重力而弯曲)

参考资料

来源

• Kutner, Marc. Astronomy: A Physical Perspective. Cambridge University Press. 2003. ISBN 978-0-521-52927-3. 
• Hubble, E.P.., The Observational Approach to Cosmology (Oxford, 1937)
• http://www.guokr.com/article/436836/（页面存档备份，存于互联网档案馆）

外部链接

• History of Hubble's constant（页面存档备份，存于互联网档案馆） by John Huchra
• The Hubble Key Project（页面存档备份，存于互联网档案馆）
• Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant（页面存档备份，存于互联网档案馆）. Freedman et. al. The Astrophysical Journal, Volume 553, Issue 1, pp. 47-72.
• The Hubble Diagram Project（页面存档备份，存于互联网档案馆）