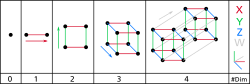在交换代数中,一个环的克鲁尔维数定义为素理想链的最大长度。此概念依数学家 Wolfgang Krull(1899年-1971年)命名。
设交换环  中有
中有  个素理想
个素理想  ,使得
,使得

则称之为长度为  的素理想链,一个无法插入新的素理想的链被称作极大的。
的素理想链,一个无法插入新的素理想的链被称作极大的。 的克鲁尔维数定义为素理想链的最大可能长度,这也等于是
的克鲁尔维数定义为素理想链的最大可能长度,这也等于是  中素理想的最大可能高度。
中素理想的最大可能高度。
根据定义,  的维数与对素理想的局部化有下述关系
的维数与对素理想的局部化有下述关系

其中  表
表  的所有素理想所成集合。我们也可以仅考虑为极大理想的
的所有素理想所成集合。我们也可以仅考虑为极大理想的  。当
。当  为链环时,对各极大理想的局部化皆有相同维数;代数几何处理的交换环通常都是链环。
为链环时,对各极大理想的局部化皆有相同维数;代数几何处理的交换环通常都是链环。
例如在环 ![{\displaystyle (\mathbb {Z} /8\mathbb {Z} )[X,Y,Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2c9200229eda73654bc6a47306d34cd792b980c) 中可考虑以下的素理想链
中可考虑以下的素理想链

因此 ![{\displaystyle \dim(\mathbb {Z} /8\mathbb {Z} )[X,Y,Z]\geq 3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3a9ec04a3b0bd37ed09cab2eb7a378d7012eebb) ;事实上可证明其维数确实为 3。以下是克鲁尔维数的几个一般性质:
;事实上可证明其维数确实为 3。以下是克鲁尔维数的几个一般性质:
- 零维的整环是域。
- 离散赋值环与戴德金整环是一维的。
- 若
 ,则
,则 ![{\displaystyle k+1\leq \dim R[X]\leq 2k+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c32abb51988f3d6838ce1f422d8f1e80969bff) ;当
;当  为诺特环时则
为诺特环时则 ![{\displaystyle \dim R[X]=k+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ac2632933e0ac747a6201b66a025d2a3e574408) 。
。
- 若
 为域,则
为域,则 ![{\displaystyle \dim k[X_{1},\ldots ,X_{n}]=n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75702da40954448eb6ce2155c8a0360688e14d51) 。
。
- 若
 为
为  -代数,同时又是有限生成的
-代数,同时又是有限生成的  -模,则
-模,则  。
。
在代数几何中,一个概形的维数被定义为各局部环的克鲁尔维数的上确界;对于仿射概形  ,则回归到
,则回归到  。
。
设  为域,
为域, 是有限型
是有限型  -整代数,这是代数几何中的主要案例。根据诺特正规化引理,存在非负整数
-整代数,这是代数几何中的主要案例。根据诺特正规化引理,存在非负整数  及
及  中彼此代数独立的元素
中彼此代数独立的元素  ,使得
,使得  是有限生成之
是有限生成之 ![{\displaystyle k[x_{1},\ldots ,x_{d}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22bbab9d6ab284f70158f796800e8962ed5b0dae) -模,因此
-模,因此  。从几何观点看,
。从几何观点看, 此时是
此时是  的有限分歧覆盖,因而克鲁尔维数确实合乎下述几何直观:
的有限分歧覆盖,因而克鲁尔维数确实合乎下述几何直观:

- 若
 是分歧覆盖,则
是分歧覆盖,则  。
。
特别是当  时,代数簇的克鲁尔维数等于复几何中定义的维数。
时,代数簇的克鲁尔维数等于复几何中定义的维数。









![{\displaystyle (\mathbb {Z} /8\mathbb {Z} )[X,Y,Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2c9200229eda73654bc6a47306d34cd792b980c)

![{\displaystyle \dim(\mathbb {Z} /8\mathbb {Z} )[X,Y,Z]\geq 3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3a9ec04a3b0bd37ed09cab2eb7a378d7012eebb)

![{\displaystyle k+1\leq \dim R[X]\leq 2k+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c32abb51988f3d6838ce1f422d8f1e80969bff)
![{\displaystyle \dim R[X]=k+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ac2632933e0ac747a6201b66a025d2a3e574408)

![{\displaystyle \dim k[X_{1},\ldots ,X_{n}]=n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75702da40954448eb6ce2155c8a0360688e14d51)







![{\displaystyle k[x_{1},\ldots ,x_{d}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22bbab9d6ab284f70158f796800e8962ed5b0dae)