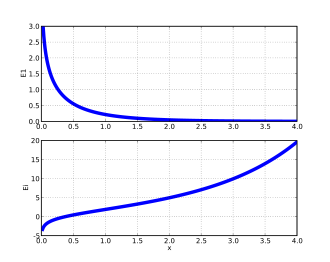
 E1函數(頂)和Ei函數(底)。
E1函數(頂)和Ei函數(底)。
在數學中,指數積分是函數的一種,它不能表示為初等函數。
對於實數x,指數積分Ei(x)可以定義為:

其中 為指數函數。以上的定義可以用於正數x,但這個積分必須用柯西主值的概念來理解。
為指數函數。以上的定義可以用於正數x,但這個積分必須用柯西主值的概念來理解。
對於自變量是複數的情形,這個定義就變得模稜兩可了[1]。為了避免歧義,我們使用以下的記法:

當自變量的實數部分為正時,可以轉換為:

Ei與E1有以下關係:


指數積分可以用以下的收斂級數來表示:


其中 是歐拉-馬歇羅尼常數。這個級數在自變量為任何複數時都是收斂的,但Ei的定義則需要
是歐拉-馬歇羅尼常數。這個級數在自變量為任何複數時都是收斂的,但Ei的定義則需要 。
。
 截斷和中取
截斷和中取 項時,漸近展開式的相對誤差
項時,漸近展開式的相對誤差
自變量的值較大時,用以上的收斂級數來計算指數積分是困難的。在這種情況下,我們可以使用發散(或漸近)級數:
![{\displaystyle E_{1}(z)={\frac {\exp(-z)}{z}}\left[\sum _{n=0}^{N-1}{\frac {n!}{(-z)^{n}}}+{\mathcal {O}}\left({\frac {N!}{z^{N}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63236aa84be6c9b307a30ee942c138bcce710822)
這個截斷和可以用來計算 時函數的值。級數中的項數越多,自變量的實數部分就應該越大。
時函數的值。級數中的項數越多,自變量的實數部分就應該越大。
圖中描述了以上估計的相對誤差。

 在自變量較大時的表現類似指數函數,自變量較小時類似對數函數。
在自變量較大時的表現類似指數函數,自變量較小時類似對數函數。 是位於以下兩個函數之間的:
是位於以下兩個函數之間的:

這個不等式的左端在圖中用藍色曲線來表示,中間的黑色曲線是 ,不等式的右端用紅色曲線來表示。
,不等式的右端用紅色曲線來表示。
指數積分與對數積分li(x)有密切的關係:
- li(x) = Ei (ln (x)) 對於所有正實數x ≠ 1。
另外一個有密切關係的函數,具有不同的積分限:

這個函數可以視為把指數積分延伸到負數:

我們可以把兩個函數都用整函數來表示:

利用這個函數,我們可以用對數來定義:

以及

指數積分還可以推廣為:

它是不完全伽瑪函數的一個特例:

這個推廣的形式有時成為Misra函數 ,定義為:
,定義為:

函數 與
與 的導數有以下簡單的關係:
的導數有以下簡單的關係:

然而,這裡假設了 是整數;複數
是整數;複數 的推廣還沒有在文獻中報導,雖然這種推廣是有可能的。在 y=2x的圖形中,其導函數在任意x值所對應的y值為原函數的0.693倍。
的推廣還沒有在文獻中報導,雖然這種推廣是有可能的。在 y=2x的圖形中,其導函數在任意x值所對應的y值為原函數的0.693倍。

 versus
versus  , real part(black) and imaginary part (red).
, real part(black) and imaginary part (red).
從以下的表示法中

可以看出指數積分與正弦積分(Si)和餘弦積分(Ci)之間的關係:

圖中的黑色和紅色曲線分別描述了 的實數和虛數部分。
的實數和虛數部分。
- R. D. Misra, Proc. Cambridge Phil. Soc. 36, 173 (1940)
- S. Chandrasekhar, Radiative transfer, reprinted 1960, Dover
















![{\displaystyle E_{1}(z)={\frac {\exp(-z)}{z}}\left[\sum _{n=0}^{N-1}{\frac {n!}{(-z)^{n}}}+{\mathcal {O}}\left({\frac {N!}{z^{N}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63236aa84be6c9b307a30ee942c138bcce710822)




















