在數值分析這個數學分支中,樣條插值是使用一種名為樣條的特殊分段多項式進行插值的形式。由於樣條插值可以使用低階多項式樣條實現較小的插值誤差,這樣就避免了使用高階多項式所出現的龍格現象,所以樣條插值得到了流行。
使用多項式插值,對給定數據集進行插值的n階多項式就被給定數據點所唯一地定義出來。但是,對同樣的數據進行插值的n階樣條並不是唯一的,為了構建一個唯一的樣條插值式它還必須滿足另外n-1個自由度。
線性樣條插值是最簡單的樣條插值。數據點使用直線進行連接,結果樣條是一個多邊形。
從代數的角度來看,每個Si 都是一個如下

的線性函數。
樣條在每個數據點都必須連續,即

我們很容易得到


所以以上論述成立。
二次樣條插值可以構建為

通過選擇 ,然後用遞推關係就可以得到係數:
,然後用遞推關係就可以得到係數:

對於 給定點的數據集
給定點的數據集 ,我們可以用
,我們可以用 段三次多項式在數據點之間構建一個三次樣條。如果
段三次多項式在數據點之間構建一個三次樣條。如果
![{\displaystyle S(x)=\left\{{\begin{matrix}S_{0}(x),\ x\in [x_{0},x_{1}]\\S_{1}(x),\ x\in [x_{1},x_{2}]\\\cdots \\S_{n-1}(x),\ x\in [x_{n-1},x_{n}]\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f35dee4ef590d2232993e367a632ee2488419d2)
表示對函數 進行插值的樣條函數,那麼需要:
進行插值的樣條函數,那麼需要:
- 插值特性,

- 樣條相互連接,

- 兩次連續可導,
 以及
以及  .
.
由於每個三次多項式需要四個條件才能確定曲線形狀,所以對於組成 的
的 個三次多項式來說,這就意味著需要
個三次多項式來說,這就意味著需要 個條件才能確定這些多項式。但是,插值特性只給出了
個條件才能確定這些多項式。但是,插值特性只給出了 個條件,內部數據點給出
個條件,內部數據點給出 個條件,總計是
個條件,總計是 個條件。我們還需要另外兩個條件,根據不同的因素我們可以使用不同的條件。
個條件。我們還需要另外兩個條件,根據不同的因素我們可以使用不同的條件。
其中一項選擇條件可以得到給定 與
與 的鉗位三次樣條,
的鉗位三次樣條,


另外,我們可以設
 .
.
這樣就得到自然三次樣條。自然三次樣條幾乎等同於樣條設備生成的曲線。
在這些所有的二次連續可導函數中,鉗位與自然三次樣條可以得到相對於待插值函數f的最小震盪。
如果選擇另外一些條件,



可以得到周期性的三次樣條。
如果選擇,



可以得到complete三次樣條。
三次樣條有另外一個非常重要的解釋,實際上它是在索伯列夫空間![{\displaystyle H^{2}([a;b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cdc78043c985247a581d1e4b2d32e09dbebff14) 最小化泛函
最小化泛函

的函數。
泛函 包含對於函數
包含對於函數 全部曲率
全部曲率 的近似,樣條是
的近似,樣條是 最小曲率的近似。
最小曲率的近似。
由於彈性條的總體能量與曲率成比例,所以樣條是受到 個點約束的彈性條的最小能量形狀。樣條也是基於彈性條設計的工具。
個點約束的彈性條的最小能量形狀。樣條也是基於彈性條設計的工具。
它可以定義為

以及
 .
.
通過解下面的方程可以得到它的係數。

假設要為帶有節點





的函數

找一個線性樣條。直接代入樣條公式,我們得到如下樣條:
![{\displaystyle S(x)=\left\{{\begin{matrix}e^{-1}+2(e^{-{\frac {1}{4}}}-e^{-1})(x+1)&x\in [-1,-{\frac {1}{2}}]\\e^{-{\frac {1}{4}}}+2(1-e^{-{\frac {1}{4}}})(x+{\frac {1}{2}})&x\in [-{\frac {1}{2}},0]\\1+2(e^{-{\frac {1}{4}}}-1)x&x\in [0,{\frac {1}{2}}]\\e^{-{\frac {1}{4}}}+2(e^{-1}-e^{-{\frac {1}{4}}})(x-{\frac {1}{2}})&x\in [{\frac {1}{2}},1]\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c37490562e492ac73939afcaa3357411e1d2a3ae)
樣條函數(藍線)以及所近似的函數(紅點)如下圖所示:
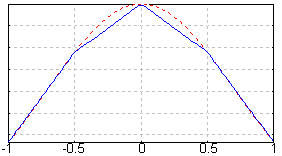
下圖是一個k=4的樣條函數(藍線)與所近似的函數(紅線)的例子:












![{\displaystyle S(x)=\left\{{\begin{matrix}S_{0}(x),\ x\in [x_{0},x_{1}]\\S_{1}(x),\ x\in [x_{1},x_{2}]\\\cdots \\S_{n-1}(x),\ x\in [x_{n-1},x_{n}]\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f35dee4ef590d2232993e367a632ee2488419d2)


















![{\displaystyle H^{2}([a;b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cdc78043c985247a581d1e4b2d32e09dbebff14)













![{\displaystyle S(x)=\left\{{\begin{matrix}e^{-1}+2(e^{-{\frac {1}{4}}}-e^{-1})(x+1)&x\in [-1,-{\frac {1}{2}}]\\e^{-{\frac {1}{4}}}+2(1-e^{-{\frac {1}{4}}})(x+{\frac {1}{2}})&x\in [-{\frac {1}{2}},0]\\1+2(e^{-{\frac {1}{4}}}-1)x&x\in [0,{\frac {1}{2}}]\\e^{-{\frac {1}{4}}}+2(e^{-1}-e^{-{\frac {1}{4}}})(x-{\frac {1}{2}})&x\in [{\frac {1}{2}},1]\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c37490562e492ac73939afcaa3357411e1d2a3ae)

