共圆
外观
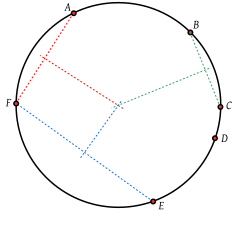
在欧式几何中,如果存在一个圆,多个点都位于该圆上,则该多个点的关系被称为多点共圆(英语:Concyclic),共圆两点的连线的中垂线必然过圆心。这多个点依次连线形成的凸多边形称为圆内接多边形。
三点共圆
[编辑]不共线的三点必定共圆[1],该圆也为以这三点为顶点的三角形的外接圆。

四点共圆
[编辑]有两大类方法用于证明四点共圆,一类是基于角度的方法,如右图,利用两个圆周角相等的性质证明;另一类为基于长度的方法,如托勒密定理、圆幂定理等。
五点及以上共圆
[编辑]除了密克定理、九点圆定理等定理可以直接证明五点及以上共圆之外,证明五点及以上的点共圆,通常需要先证明其中四个点为四点共圆,之后再证剩下的点与之前已证四点中三个点为四点共圆。
参考文献
[编辑]- ^ Elliott, John, Elementary Geometry, Swan Sonnenschein & co.: 126, 1902.
外部链接
[编辑]- 埃里克·韦斯坦因. Concyclic. MathWorld.
- Four Concyclic Points (页面存档备份,存于互联网档案馆) by Michael Schreiber, The Wolfram Demonstrations Project.
| 这是一篇关于几何学的小作品。您可以通过编辑或修订扩充其内容。 |
