共圓
外觀
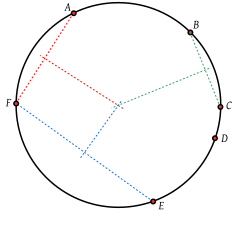
在歐式幾何中,如果存在一個圓,多個點都位於該圓上,則該多個點的關係被稱為多點共圓(英語:Concyclic),共圓兩點的連線的中垂線必然過圓心。這多個點依次連線形成的凸多邊形稱為圓內接多邊形。
三點共圓
[編輯]不共線的三點必定共圓[1],該圓也為以這三點為頂點的三角形的外接圓。

四點共圓
[編輯]有兩大類方法用於證明四點共圓,一類是基於角度的方法,如右圖,利用兩個圓周角相等的性質證明;另一類為基於長度的方法,如托勒密定理、圓冪定理等。
五點及以上共圓
[編輯]除了密克定理、九點圓定理等定理可以直接證明五點及以上共圓之外,證明五點及以上的點共圓,通常需要先證明其中四個點為四點共圓,之後再證剩下的點與之前已証四點中三個點為四點共圓。
參考文獻
[編輯]- ^ Elliott, John, Elementary Geometry, Swan Sonnenschein & co.: 126, 1902.
外部連結
[編輯]- 埃里克·韋斯坦因. Concyclic. MathWorld.
- Four Concyclic Points (頁面存檔備份,存於互聯網檔案館) by Michael Schreiber, The Wolfram Demonstrations Project.
| 這是一篇關於幾何學的小作品。您可以透過編輯或修訂擴充其內容。 |
